OEAW-Logo RICAM-Logo
Special Radon Semester on Computational Mechanics
Linz, October-December 2005
Home Scientific OverviewThematic Structure Time ScheduleSpecial EventsParticipantsPublicationsFollow-up Events
Ricam
"Discontinuous Galerkin methods" organized by Raytcho Lazarov

Up: L_Schedule Previous: Miniworkshop on DG methods

Bibliography

1
D. Arnold, F. Brezzi, B. Cockburn and D. Marini, Unified analysis of discontinuous Galerkin methods for elliptic problems, SIAM J. Numer. Anal., 39 (2002), 1749-1779. (http://epubs.siam.org/sam-bin/dbq/article/38416)

2
I. Babuška and M. Zlamal, Nonconforming elements in the finite element method with penalty, SIAM J. Numer. Anal., 10 (1973), 863-875.

3
F. Bassi and S. Rebay, A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations, J. Comput. Phys., 131 (1997), 267-279.

4
C.E. Baumann and J.T. Oden, A discontinuous 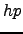$ hp$ finite element method for convection-diffusion problems, Comput. Methods Appl. Mech. Engrg., 175 (1999), 311-341.

5
C.E. Baumann and J.T. Oden, A discontinuous 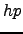$ hp$ finite element method for the Euler and Navier-Stokes equations, Intl. J. Num. Methods in Fluids, 31 (1999), 79-95.

6
S. Brenner and L. Sung, $ C^0$ interior penalty methods for fourth order elliptic boundary value problems on polygonal domains, Journal of Scientific Computing, 22-23 (2005), 83-118

7
S. Brenner and L. Sung, Multigrid algorithms for $ C^0$ interior penalty methods, Preprint 2004, available from http://www.math.sc.edu/$ \sim$fem/papers/DGMG4.html

8
S. Brenner and J. Zhao, Convergence of multigrid algorithms for interior penalty methods, Applied Numer. Anal. Comput. Math., 2 (1) (2005), 3-18.

9
F. Brezzi, B. Cockburn, D.L. Marini, and E. Süli, Stabilization mechanisms in discontinuous Galerkin finite element methods, Oxford University Computing Laboratory, Numerical Analysis Group Research Report NA-04/24, September 2004, 23 pages (http://web.comlab.ox.ac.uk/oucl/publications/natr/na-04-24.html)

10
B. Cockburn, Discontinuous Galerkin methods, Z. Angew. Math. Mech., 83(11) (2003), 731-754

11
B. Cockburn and J. Gopalakrishnan, New hybridization techniques, GAMM Publications, 2005 http://www.math.ufl.edu/ jayg/pub/gamm.pdf

12
B. Cockburn, J. Gopalakrishnan, and R. Lazarov, Unified hybridization of DG, mixed and conforming methods for second order elliptic problems, (in preparation).

13
B. Cockburn, G. Kanschat, and D. Schötzau, Local DG method for the Oseen equations, Math. Comp., 2005.

14
B. Cockburn, G. Kanschat, D. Schötzau and C. Schwab, Local discontinuous Galerkin methods for the Stokes system, SIAM J. Numer. Anal., 40 (2002), 319-343.

15
B. Cockburn, G. Kanschat, and D. Schötzau, The local discontinuous Galerkin methods for incompressible fluid flow: A review, Computer and Fluids (Special Issue: Residual based methods and discontinuous Galerkin schemes), 34 (2005), 491-506.

16
B. Cockburn, G.E. Karniadakis, and C.W. Shu (eds.): The Discontinuous Galerkin Methods: Theory, Computation and Applications, Lecture Notes in Computational Science and Engineering, Volume 11, Springer-Verlag, 2000.

17
B. Cockburn and C.W. Shu, The local discontinuous Galerkin finite element method for convection-diffusion systems, SIAM J. Numer. Anal., 35 (1998), 2440-2463.

18
J. Douglas, Jr. and T. Dupont, Interior penalty procedures for elliptic and parabolic Galerkin methods, Lecture Notes in Physics, 58, Springer-Verlag, Berlin, 1976.

19
J. Douglas, Jr. and J. Wang, An absolutely stabilized finite element method for the Stokes problem, Mathematics of Computation, 52 (1989) 495-508.

20
R.E. Ewing, J. Wang, and Y. Yang, A stabilized discontinuous finite element method for elliptic problems, Numer. Lin. Alg. Appl., 10 (2003), 83-104.

21
V. Girault, B. Rivière, and M.F. Wheeler, A discontinuous Galerkin method with nonconforming domain decomposition for Stokes and Navier-Stokes problems, Math. Comp., 74 (249) (2004), 53-84.

22
J. Gopalakrishnan and G. Kanschat, A multilevel discontinuous Galerkin method, Numerische Mathematik, 95 (3), 527-550, 2003.

23
P. Hansbo and M.G. Larson, Discontinuous Galerkin methods for incompressible and nearly incompressible elasticity by Nitsche's method, Comput. Meth. Appl. Mech. Engng., 191 (2002) 1895-1908.

24
C. Johnson, Finite element methods for PDE, Cambridge University Press, 1994.

25
K. Johannsen, A symmetric smoother for the nonsymmetric interior penalty discontinuous Galerkin discretization, ICES Report 05-23, University of Texas at Austin, 2005 (submitted to Numerical Linear Algebra with Applications).

26
G. Kanschat and R. Rannacher, Local error analysis of the interior penalty discontinuous Galerkin method for second order elliptic problems, J. Numer. Math., 10 (4), (2002), 249-274.

27
R.M. Kirby, T.C. Warburton, I. Lomtev and G.E. Karniadakis, A discontinuous Galerkin spectral/hp method on hybrid grids, Applied Numerical Mathematics, 33, 2000, 393-405.

28
R. Lazarov. P. Vassilevski, and L. Zikatanov, Optimal preconditioning of some discontinuous Galerkin methods for second order elliptic problems, Preprint 2005.

29
R. Lazarov and X. Ye, Stabilized discontinuous finite element approximations for Stokes equations, ISC Tecnical Report, ISC-05-04-MATH (http://www.isc.tamu.edu/tr/0504.pdf)

30
Igor Lomtev and George E. Karniadakis, A Discontinuous Galerkin Method for the Navier-Stokes Equations, Intl. J. Num. Methods in Fluids, 29, (1999), 587-603.

31
I. Lomtev, R.M. Kirby and G.E. Karniadakis, A Discontinuous Galerkin ALE Method for Compressible Viscous Flows in Moving Domains, J. Comput. Phys., 155, (1999), 128-159.

32
J.A. Nitsche, Über ein Variationsprinzip zur Lösung Dirichlet-Problemen bei Verwendung vonTeilräumen, die keinen Randbedingen unteworten sind, Abh. Math. Sem. Univ. Hamburg, 36 (1971), 9-15.

33
W.H. Reed and T. R. Hill, Triangular mesh methods for the neutron transport equation, Tech Report LA-UR-73-479, Los Alamos Scientific Laboratory, 1973.

34
B. Rivière, M.F. Wheeler, and V. Girault, A priori error estimates for finite element method based on discontinuous approximation spaces for elliptic problems. SIAM J. Numer.Anal., 39 (3) (2001), 902-931.

35
J. Wang, and X. Ye, A new finite element method for Stokes equation by 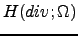$ H(div;\Omega)$ elements, Tech Report 99-09, TICAM, 1999.


Satyendra Tomar 2005-08-18

Back
URL: www.ricam.oeaw.ac.at/specsem/sscm/structure/lazarov/node6.php

This page was made with 100% valid HTML & CSS - Send comments to Webmaster
Today's date and time is 04/24/24 - 20:22 CEST and this file (/specsem/sscm/structure/lazarov/node6.php) was last modified on 03/16/16 - 13:43 CEST

Impressum