|
 |
 |
 |
 |
Gröbner Basis Implementations
The database Gröbner Bases Implementations. Functionality Check and Comparison describes functionality of computer algebra systems,
making an emphasis on the details of implementations of Buchberger's Gröbner Basis algorithm, its generalizations and alternatives.
|
 |
 |
Proceedings of the Special Semester on Gröbner Bases
As a result of the workshops, we agreed to have 10 volumes of proceedings, which will be published with three different publishers.
In case you want to submit papers to any of the volumes, please, see the respective call for paper and get in contact with the respective managing editor.
Here is a list of the 10 volumes with their guest editors:
- Nr. 1, Working Title: "Approximate Commutative Algebra"
- Nr. 2, Working Title: "Efficient Computation of Gröbner Bases"
- Editors: J.C. Faugere, H.G. Graebe, V. Levandovskyy, Q.N. Tran
- Managing Editor: Q. N. Tran
- Publisher: Journal of Symbolic Computation Special Issue (Elsevier)
- CfP: Download pdf
- Style Files: JSC_LaTex_Style.zip
- Nr. 3, Working Title: "Polynomial Systems Solving"
- Editors: J.C. Faugere, F. Roullier
- Managing Editor: J.C. Faugere
- Publisher: RISC book series (Springer Heidelberg)
- CfP: Available soon
- Nr. 4, Working Title: "Gröbner Bases, Coding, and Cryptography"
- Editors: T. Mora, L. Perret, S. Sakata, M. Sala, C. Traverso
- Managing Editor: M. Sala
- Publisher: RISC Book Series (Springer, Heidelberg)
- CfP: Call for Papers
- Nr. 5, Working Title: "Gröbner Bases, Coding, and Cryptography"
- Nr. 6, Working Title: "Algorithmic Algebraic Combinatorics and Gröbner Bases"
- Editors: G. Jones, A. Jurisic, M. Muzychuk, I. Ponomarenko
- Managing Editor: G. Jones
- Coordination: M. Klin
- Publisher: RISC Book Series (Springer, Heidelberg)
- CfP: Call for Papers
- Nr. 7, Working Title: "Gröbner Bases in Symbolic Analysis"
- Nr. 8, Working Title: "Gröbner Bases, Control Theory and Signal Processing"
- Nr. 9, Working Title: "Non-commutative Gröbner Bases"
|
 |
 |
Conducted Work
- U. Oberst, M. Scheicher: A Survey of (BIBO) Stability and (Proper) Stabilization of Multidimensional Input/Output Systems. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
- G. Carrá Ferro: A Survey on Differential Gröbner Bases. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- G. Regensburger: Applications of filter coefficients and wavelets parametrized by moments. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
- L. Xu: Applications of Gröbner Bases in Synthesis of Multidimensional Control Systems. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
- A. Fabianska, A. Quadrat: Applications of the Quillen-Suslin theorem to multidimensional systems theory. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
- K. Krupchyk, J. Tuomela: Compatibility Complexes for Overdetermined Boundary Problems. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- A. Levin: Computation of the Strength of Systems of Difference Equations via Generalized Gröbner Bases. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- B. Paláncz: Computer Algebra in Geodesy Resection N-points problem. Applied Mathematica: Proceedings of 8th International Mathematica Symposium, CD edition, Editor Yves Papegay, Published by INRIA, Rocquencourt, France, ISBN 2-7261-1289-7
- F. Boulier: Differential Elimination and Biological Modelling. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- P. Olver, J. Pohjanpelto: Differential Invariants for Lie Pseudo-groups. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- S.A. Abramov, M. Petkovsek: Dimensions of Solution Spaces of H-Systems. Submitted to Journal of Symbolic Computation.
- J.-F. Pommaret: Gröbner bases in algebraic analysis: New perspectives for applications In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- W. N. Traves: Invariant Theory and Differential Operators. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- D. Robertz: Janet Bases and Applications. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- X. Chen, V. G. Romanovski, W. Zhang: Linearizability conditions of time-reversible quartic systems having homogeneous nonlinearities. Journal of Nonlinear Analysis: Theory, Methods & Applications, In Press, Corrected Proof, Available online 21 July 2007.
- R. L. McCasland, A. Bundy: MATHsAiD: a Mathematical Theorem Discovery Tool. Proceedings of SYNASC 2006, pp17-22, IEEE Computer Society Press, 2006.
- J. Lebrun: Normal Forms in Statistical Signal Processing. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
- V. Levandovskyy, E. Zerz: Obstructions to Genericity in Study of Parametric Problems in Control Theory. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
- M. Wang: On factor prime factorizations for n-D polynomial matrices. IEEE Transactions on Circuits and Systems-I, Regular papers, vol.54, No. 6, June 2007, 1398-1405.
- F. L. Pritchard, W. Y. Sit: On Initial Value Problems for Ordinary Differential-Algebraic Equations. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- R. Zaare-Nahandi: On isomorphism of simplicial complexes and related algebras. Submitted to Journal of Symbolic Computation.
- W. Castro: On methods for the construction of reduction rings. Submitted to Journal of Symbolic Computation.
- M. Peng, N. K. Bose: Parametrized Biorthogonal Wavelets and FIR Filter Bank Design with Gröbner Bases. Submitted to SIAM Journal of Numerical Analysis.
- M. Wang: Remarks on n-D polynomial matrix factorization problems. Submitted to IEEE Transactions on Circuits and Systems -II.
- U. Oberst, F. Pauer: Solving Systems of Linear Partial Difference and Differential Equations with Constant Coefficients Using Gröbner Bases. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- W. M. Seiler: Spencer Cohomology, Differential Equations, and Pommaret Bases. In: "Gröbner Bases in Symbolic Analysis" (M. Rosenkranz, D. Wang eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019323-7.
- E. Zerz: State representations of time-varying linear systems. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
- H.C. Graf von Bothmer, O. Labs, J. Schicho, C. van de Woestijne: The Casas-Alvero conjecture for infinitely many degrees.
- X. Chen, D. Wang: Towards an Electronic Geometry Textbook. Presented at the Sixth International Workshop on Automated Deduction in Geometry 2006 (ADG2006), University of Vigo, Spain.
- N.K. Bose: Two Decades (1985-2005) of Gröbner Bases in Multidimensional Systems. In: "Gröbner Bases in Control Theory and Signal Processing" (H. A. Park, G. Regensburger eds.), Radon Series on Computational and Applied Mathematics, de Gruyter, ISBN 978-3-11-019333-6.
|
 |
 |
Objective
The algorithmic theory of Gröbner bases has been introduced, in 1965, by Bruno Buchberger with various forerunners since the end of the 19th century and various related theories. In the meantime, the method of Gröbner bases has been heavily studied and is now available in all major mathematical software systems. It has found numerous applications in abstract fields of mathematics as well as in science and engineering.
The special semester on Gröbner bases aims at bringing together researchers from all over the world for joint research on Gröbner bases and related theories and methods. Also, through the special semester, knowledge on these theories should be made availabe and disseminated in a new way that uses both recent advances in formalized mathematics as well as web technology. Part of the effort during the special semester will also go into special lectures, tutorials, and training and, after the special semester, events for the dissemination of the research results will be organized. Both established researchers as well as junior researchers, postdocs, and PhD students are welcome to participate in the activities of the special semester.
If you are interested in participating in the special semester, send the application form. Note that, through formulating proposals in the application form, you may significantly influence the program of the special semester.
|
 |

Wolfgang Gröbner (1899-1980)
|
 |
 |
Program Committee
Jean-Charles Faugère, UPMC, France
Vladimir P. Gerdt, JINR, Russia
Gert-Martin Greuel, University of Kaiserslautern, Germany
Hoon Hong, NCSU, USA
Daniel Lazard, LIP6 and project SALSA (INRIA), France
Hyungju Park, KIAS, Korea
Lorenzo Robbiano, University of Genova, Italy
Jose Luis Ruiz Reina, University of Seville, Spain
Hans J. Stetter, TU Vienna, Austria
Quoc-Nam Tran, Lamar, USA
Carlo Traverso, University of Pisa, Italy
Dongming Wang, UPMC, France
Franz Winkler, RISC, Austria
Kazuhiro Yokoyama, Rikkyo University, Japan
|
 |

The RICAM group
|
 |
 |
Significance
The significance of the Gröbner bases theory and method and of similar theories is documented by the following facts:
- An extra entry in the MSC classification of mathematics is devoted to Gröbner Bases: 13P10.
- So far, approx. 600 publications and 10 textbooks have been devoted to Gröbner Bases.
- Gröbner Bases are routinely available in all current mathematical software systems like Mathematica, Maple, Derive, Magma, Axiom, etc.
- Special software systems, like CoCoa, Macaulay, Singular, Plural, Risa-Asir etc. are, to a big extent, devoted to the applications of Gröbner Bases.
- Gröbner Bases theory is an important section in all international conferences on computer algebra and symbolic computation.
- Gröbner Bases allow, for the first time, algorithmic solutions to some of the most fundamental problems in algebraic geometry but are applied also in such diverse areas as functional analysis, statistics, optimization, coding theory, cryptography, automated theorem proving in geometry, graph theory, combinatorial identities, symbolic summation, special functions, etc.
- Since non-linear systems are ubiquitous in all natural and technical sciences, the Gröbner bases and related methods have numerous applications in science and engineering.
|
 |

The RICAM building in Linz
|
 |
 |
Research Focus
Gröbner bases and related theories are already a big field. Therefore, in order to enhance the chance of coming up with new research results during the semester, we will focus on a few research directions that seem to be particularly topical and innovative:
- Formal Gröbner bases theory: build-up of web-accessible formal knowledge base verified by automated reasoners, formal computer-supported verification and synthesis of algorithms in Gröbner bases and related theories, generic and generalized versions of the theory, formal reasoning methods for Gröbner bases and related theories.
- Efficient implementation of Gröbner bases and related algorithms: theoretical foundation of new versions of the algorithms; best practice of implementation; comparative complexity and computing time analysis; interplay with numerics; interplay with algorithms in real algebraic geometry; systems clinics.
- Recent and new applications of the theory: applications in operator theory (functional analysis) as a frame for applications for differential equations, recurrence relations, special function theory etc.; applications in coding theory and cryptography; applications in graph theory; etc.
Other focus directions may be accepted as a result of the discussion process between now and the start of the special semester in February 2006 (see application).
|
 |

Castle of Hagenberg | Austria
|
 |
 |
Collateral Activities
In preparation of, during, and after the special semester the following activities will be organized in order to establish a long-term effect of the special semester:
- Build-up of a formal knowledge (and algorithm) base for Gröbner bases and related theories (in the frame of the Theorema system); see knowledge.
- Build-up of a web-accessible papers data base for Gröbner bases and related theories, see bibliography.
- Build-up of a service center for problem solving on the bases of Gröbner bases and related theories, see service.
|
 |

Castle of Hagenberg | Austria
|
 |
 |
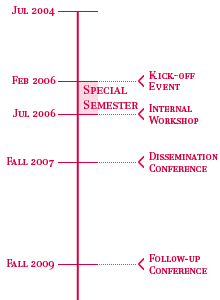
Schedule
- Preparatory phase: April 2005 - February 2006
- Worldwide announcement of special semester.
- Invitation / application of senior and junior visiting researchers, postdocs, graduated students.
- Build-up of date base of web-accessible, downloadable papers.
- Organization of special workshops during the semester.
- Internal seminars.
- Contributions of the visiting researchers to the build-up of the papers data base and the formalized knowledge base.
- End of July 2006: Internal Workshop "Progress Report on Gröbner Bases and Related Theories".
- Follow up phase: July 2006 - ...
- Running of the Information Center on Gröbner Bases and related methods.
- Fall 2007: International Conference on Gröbner Bases and Applications (in connection and coordination with Computer Algebra Application conferences and related conferences and collocated with MEGA 2007 at RISC).
- Presentation of the scientific results of the special semester and the worldwide research stimulated by the special semester.
- Tutorials on the Gröbner Bases method and related methods for mathematicians.
- Tutorials on the applications of Gröbner Bases and Gröbner Bases software for the industry.
- Bi-annual conference on Gröbner Bases and related methods starting from 2009.
|
 |
|
 |
 |
Poster
Download the poster of the special semester.
|
 |
 |
Local Organization
|
 |
|
 |
|
|
|
Information | Application | Program | Location | Bibliography | Knowledge | Service| Links |
|
 Webmaster Webmaster |
|